"""
Hrvoje Peradin, Valentina Vincek
"""
|
|
#Ovo su sve načini na koje možemo stvoriti prsten polinoma nad nekim poljem
#Prsten=PolynomialRing(QQ,'x')
#Prsten=PolynomialRing(QQ,'x,y,z')
#Prsten=PolynomialRing(QQ,3,'x,y,z')
#Prsten=QQ['t']
#Prsten.<t>=QQ['t']
#Prsten.<t>=QQ[]
|
|
#Konstrukcija prstena nad poljem Q, u varijabli t
Prsten=PolynomialRing(QQ,'t');
Prsten
Univariate Polynomial Ring in t over Rational Field |
# t ne možemo koristiti dok ga ne pridružimo nekom simbolu
neki_simbol=Prsten.0
neki_simbol
t |
# ali taj simbol se smije zvati i t:
t=Prsten.0
t
t |
poly=t^2+3*t+1
poly.variables()
(t,) |
poly.degree()
2 |
poly in Prsten
True |
p1=(t^3+2*t^2+3*t+4);
p2=(3*t^2+2*t+1);
|
|
p1 in Prsten, p2 in Prsten
(True, True) |
#Zbrajanje radi bez problema i na polinomima različitih stupnjeva (za razliku od Matlaba. ovdje reprezentacija nije matrična)
p1+p2
t^3 + 5*t^2 + 5*t + 5 |
#Množenje također
p1*p2
3*t^5 + 8*t^4 + 14*t^3 + 20*t^2 + 11*t + 4 |
#Prsten je zatvoren na te operacije
(p1+p2) in Prsten, (p1*p2) in Prsten
(True, True) |
#Dijeljenje
p2/p1
(3*t^2 + 2*t + 1)/(t^3 + 2*t^2 + 3*t + 4) |
# Ako p1 ne dijeli p2, onda dijeljenje konstruira element Fraction field
(p2/p1).parent()
Fraction Field of Univariate Polynomial Ring in t over Rational Field |
#ako p1|p2
(t^2-1)/(t-1)
t + 1 |
#Ostatak pri dijeljenju
p3=t^2-1
p4=t+2
p3.mod(p4)
3 |
#nzm:
gcd(t^2-1,t-1)
t - 1 |
#Vrijednost polinoma u desetak točaka
[p1(i) for i in range(10)]
[4, 10, 26, 58, 112, 194, 310, 466, 668, 922] |
#potenciranje
p1^5
t^15 + 10*t^14 + 55*t^13 + 220*t^12 + 690*t^11 + 1772*t^10 + 3830*t^9 + 7040*t^8 + 11085*t^7 + 14970*t^6 + 17203*t^5 + 16660*t^4 + 13280*t^3 + 8320*t^2 + 3840*t + 1024 |
#Derivacije i integrali
p1.derivative(t)
3*t^2 + 4*t + 3 |
p1.derivative(t)
3*t^2 + 4*t + 3 |
p1.derivative(t,2)
6*t + 4 |
p1.integral()
1/4*t^4 + 2/3*t^3 + 3/2*t^2 + 4*t |
Prsten(t^4)==t^4
True |
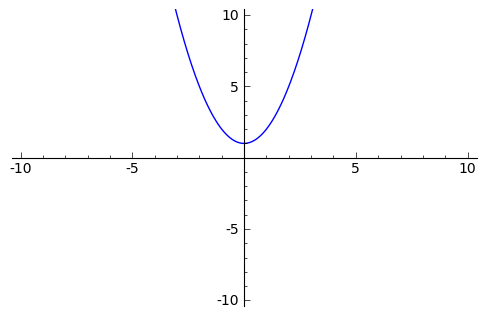
plot(Prsten(t^2+1),ymin=-10, ymax=10, xmin=-10, xmax=10)
|
|
#Nultočke (rezutat je lista parova (nultočka, kratnost) )
(t^2+4*t+4).roots()
[(-2, 2)] |
(t^2+1).roots()
[] |
(t^2+1).roots(CC)
[(-1.00000000000000*I, 1), (1.00000000000000*I, 1)] |
(t^2-1).real_roots()
[-1.00000000000000, 1.00000000000000] |
(t^2+1).complex_roots()
[-1.00000000000000*I, 1.00000000000000*I] |
f(t)=t^2+1
solve(f(t)==0,t)
[t == -I, t == I] |
f(t) in Prsten
Traceback (click to the left of this block for traceback) ... NameError: name 'f' is not defined |
#Prsteni polinoma više varijabli
R, (x,y,z) = QQ['x,y,z'].objgens()
|
|
#Funkcija objgens vraća uređenu dvojku koja sadrži prsten, i n-torku varijabli
QQ['x,y,z'].objgens()
(Multivariate Polynomial Ring in x, y, z over Rational Field, (x, y, z)) |
R
Multivariate Polynomial Ring in x, y, z over Rational Field |
#Možemo definirati prsten u više varijabli, s automatskom numeracijom svake od njih
R=PolynomialRing(QQ, 10, 'w')
R
Multivariate Polynomial Ring in w0, w1, w2, w3, w4, w5, w6, w7, w8, w9 over Rational Field |
# Možemo precizirati uređaj u kojem će se prikazivati koeficijenti (default je degrevlex
R=PolynomialRing(QQ,'a,b,c,d',order='degrevlex')
a=R.0
b=R.1
c=R.2
d=R.3
p=d*(c^3)+a*d^4+a^7+b*d+c^5+a^5+a^2*d^3
p
a^7 + a^5 + c^5 + a^2*d^3 + a*d^4 + c^3*d + b*d |
R=PolynomialRing(QQ,'a,b,c,d',order='deglex')
a=R.0
b=R.1
c=R.2
d=R.3
p=d*(c^3)+a*d^4+a^7+b*d+c^5+a^5+a^2*d^3
p
a^7 + a^5 + a^2*d^3 + a*d^4 + c^5 + c^3*d + b*d |
R=PolynomialRing(QQ,'a,b,c,d',order='lex')
a=R.0
b=R.1
c=R.2
d=R.3
p=d*(c^3)+a*d^4+a^7+b*d+c^5+a^5+a^2*d^3
p
a^7 + a^5 + a^2*d^3 + a*d^4 + b*d + c^5 + c^3*d |